回转壳体应力分析

回转壳体应力分布图如下：

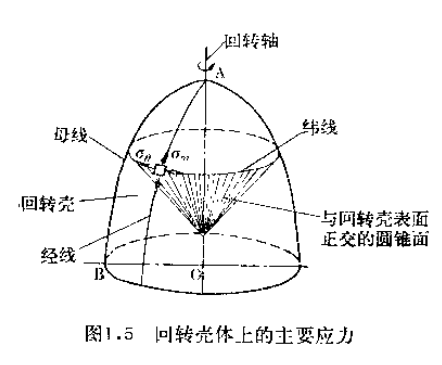
回转壳体承受内压之后，其经线和纬线方向都要发生伸长变形，因而在经线方向产生经向应力，用σm表示，在纬线方向产生环向应力，用σθ表示。

下面分别分析经向应力与环向应力：

一：经向应力分析，应力分布如下图

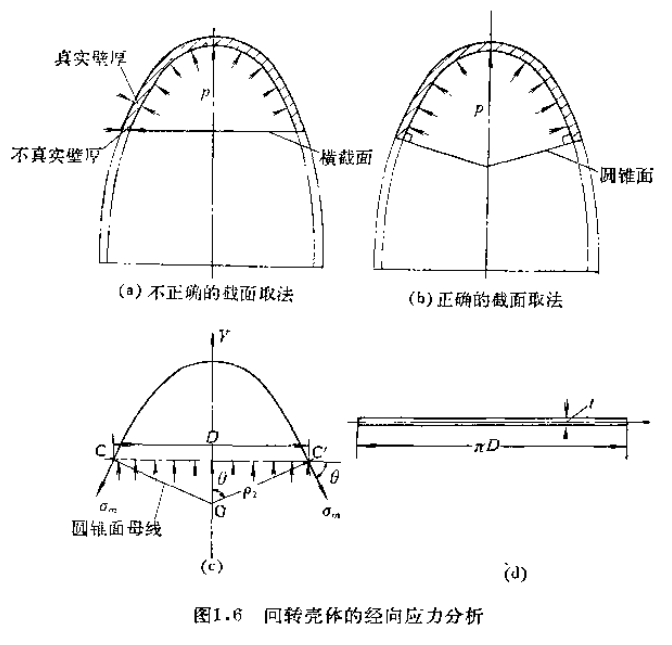
图中ρ2为第二曲率半径

圆锥面将壳体分成两部分，考虑其中任意一部分的平衡，如图1.6(c)所示。根据y方

向的平衡条件，得到

    p*π*D^2/4-σm*π*D*t* sinθ=0

D与ρ2之间存在下列关系：

ρ2=D/2sinθ代入上式得到

σm=p*ρ2/(2t)

二：环向应力分析

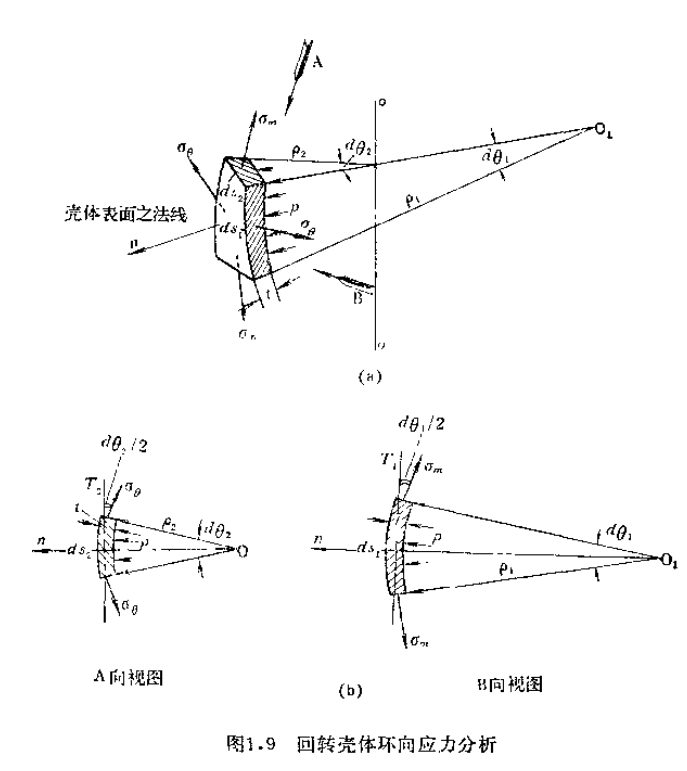
第一项Pn，内压p的合力为

P =p*ds1*ds2.

其中：ds1 =ρ1*dθ1  ds2 =ρ2*dθ2代入上式：

P= p*ρ1*dθ1*ρ2*dθ2即Pn= p*ρ1*dθ1*ρ2*dθ2

第二项Nθn：这一项借助于图1.9(b)之A向视图进行计算。因为环向应力在其作

用面上均匀分布，所以，这个面的内力

Nθ=σθ*ds1*t=σθ*ρ1*dθ1*t

Nθn=-2*σθ*ρ1*dθ1*t*sin(dθ2/2)与n方向相反

因为dθ2/2很小，sin(dθ2/2)≈dθ2/2因而得到：

Nθn=–σθ*ρ1*dθ1*t* dθ2

第三项Nmn：这一项借助于图1.9(b)的B向视图进行计算。首先求得内力

Nm=σm*ds2*t=σm*ρ2*dθ2*t

其在法线n上的投影：

     Nmn=-σm*ρ2*dθ2*t*dθ1

由法线n上的平衡方程：

     Pn+ Nθn+ Nmn=0得到

σm/ρ1+σθ/ρ2=p/t

此为计算回转壳体的一半计算公式。

若母线曲线方程为y=y(x)则第一曲率半径为：

     ρ1=((1+y’^2)^1.5)/y’’

以上定性分析与定量计算都建立在薄膜理论基础上。