薄壁容器的应力分析

本文介绍薄壁容器的应力分析：

定义：K=Dw/Dn≤1.1~1.2 

Dw容器外径；Dn容器内径。我们接触到的通常都是薄壁容器。

在内压P作用下圆筒内的受力情况如下图：

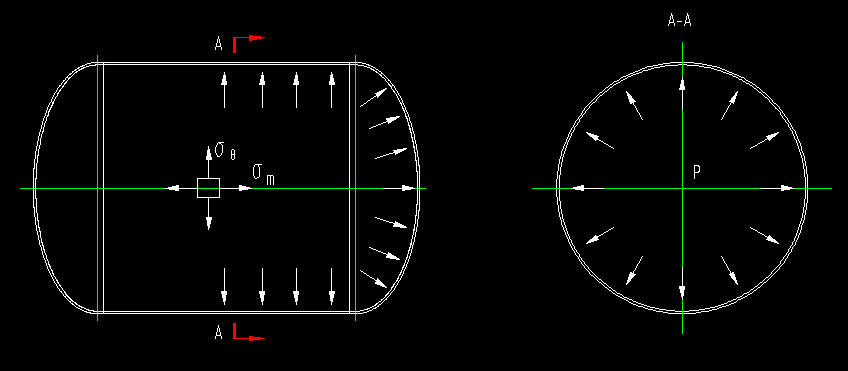
在内压p的作用下，任意一点都将产生两个方向的应力，一是由于圆筒两端的拉力产生的轴向拉应力，称为“经向应力”或“轴向应力”，用σm表示；二是由于圆筒均匀向外膨胀，在圆周切线方向产生的拉应力，称为“切向应力”或“环向应力”，用σθ表示。下面分布介绍两种应力的计算方法。

1：轴向应力计算

采用“截面法”。假想从A-A将圆筒切开，考虑其中一半的受力情况，如下图

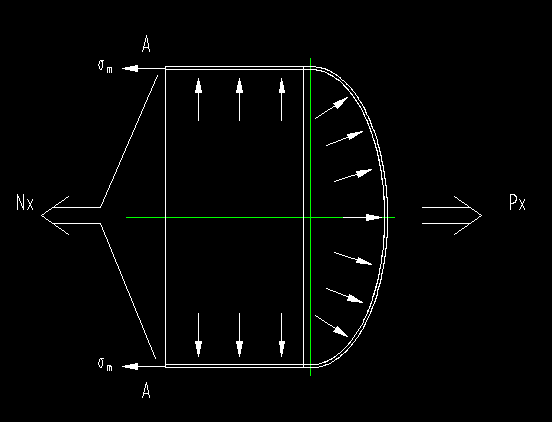
Px为内压P作用在封头上的压力，Nx为作用在截面上的内力总和。

Px=p*π*D^2/4  

Nx=σm*π*D*t 

式子中：D为平均直径mm，t为圆筒的厚度mm。

由力平衡关系Px=Nx得到：p*π*D^2/4=σm*π*D*t由此推导出σm= p*D/(4*t)

厚度计算公式为t=p*D/(4*σm)。

2 环向应力的计算

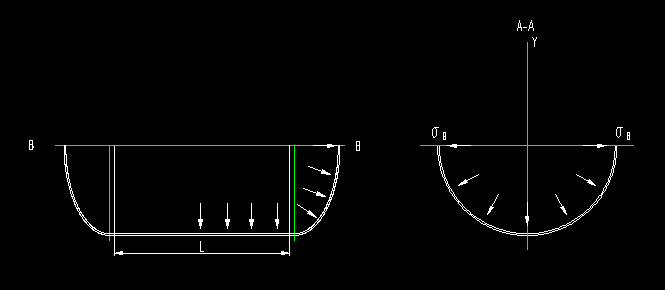
Py为内压在Y轴上的投影之和，

Py=pLD

Nθ为纵向截面的应力之和

Nθ=σθ*L*t*2

由力平衡关系Py =Nθ得到：σθ=p*D/(2*t)

厚度计算公式为t=p*D/(2*σθ)

由以上两个式子可以看出环向应力是轴向应力的两倍，所以在圆筒上开孔应该开成椭圆形的形状，如下图的样子：